How longditudinal waves can be polarised.

Light waves, when they are not absorbed, bounce off some materials and go straight through others, largely depending on whether the spaces inside the materials are large enough to allow a complete wavelength through. However, there are some materials, for instance, polarised glass or crystals, that only let part of the light wave through – they have gaps wide enough in one dimension to let a whole wave through but too narrow in the other. The result is ‘Polarised Light’, which has considerable importance in physics, not least in its role providing the first proof of entanglement.’

It is widely believed that only transverse waves can be polarised. This is for a visually obvious reason that we can summarise crudely as follows: ‘sideways waves’ are two-dimensional so can move mostly up-and-down or mostly side-to-side. Polarisation is the process that allows only one of these through. It appears that longitudinal waves go back-and-forwards in only one dimension, so there is no way to split them in two by cutting out one dimension. This turns out not to be right but how longitudinal waves can be polarised takes a long explanation, as we see below.

We can picture polarisation as like a rope wave going through a horizontal Venetian blind. A vertical rope wave, made by wiggling one end of the rope up and down, smacks into the slats of the blind and bounces back, whilst a horizontal rope wave, made by wiggling the end of the rope side-to-side, simply flows through the Venetian blind untroubled. In this way, light that passes through the polariser wiggles in one plane only.  This description of polarisation is fine for transverse waves that oscillate sideways to the direction of travel of the wave, like water waves. But longitudinal waves vary in the same direction as the wavefront moves, with no variation in any other axis, up and down or side to side. So how can this kind of wave be polarised?

In air, molecules are zooming around and crashing into each other. Relative to a transverse sound wave passing through, we can take a single molecule of air and describe its movement in three axes: forwards/backwards, left/right, and up/down. The sound wave is a pattern formed by only one aspect of this molecule’s movement, the forwards/backwards part. The kinetic energy passed from one molecule to the next in the direction that the wave is travelling causes the thinning and thickening of the air that makes up the sound wave. However, the air molecules have other aspects to their movement. Let us split the air molecules into two equal types, those with more vertical than sideways movement, and those where the opposite is true. As the sound wave approaches the Venetian blind, the ‘more-horizontal-movement-than-vertical-movement’ molecules will essentially be unaffected by the horizontal slits of the blind, while the ‘more vertical than horizontal movement’ molecules will bounce off it. Coming out the other side of the blind, the emerging sound wave will have half the energy and be polarised[1], while the other half bounce back.

This is the process of longitudinal F-wave polarisation. In many ways, it is not the wave that is being polarised but the elements of the field through which the wave is running – but that applies to the wave itself as well; it is a pattern in the field. The effect is that the light wave passing through such a material is made up of bits of field only moving in (or close to) two planes (that is back-and-forth as a wave and in only one of the other two planes), i.e. it is polarised, and the remainder of the light bounces back off the polariser.

We can go further. If part of an F-wave is polarised, the whole spherical wavefront is polarised, even the opposite side. Showing this to be the case is one of the key demonstrations of ‘entanglement’. (This used to be described as ‘two entangled particles’ that are detected non-locally, rather than one wavefront that is absorbed at two places, separated non-locally.)

Going even further we can show that a lateral wave is not possible in a 3-D environment without there being an existing 2-D surface, like water, or pseudo 1-D line, such as a rope, for it to wave on. Consequently F-waves must be longitudinal waves.

[1] In practice, audible sound waves in air are far too long for this to work – middle C is 1.3 metres long which compares to the typical distance between air molecule collisions (the ‘mean free path’), about 6×10^-8m. However, there are examples: The Polarization of Sound. An Examination into the Nature of Vibrations in Extended Media SW Robinson, Science magazine, Vol. 2, No. 46, May 14, 1881

To illustrate why consider a classic transverse wave, like the sine wave below:

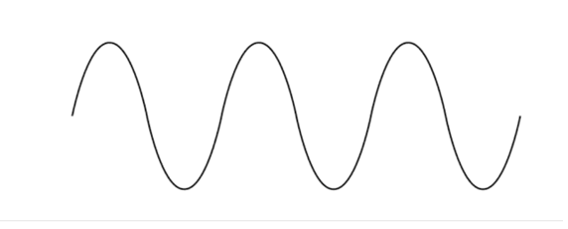
In a 3-D environment, this can be considered as a thin vertical slice from a wave. In 3-D reality, it is coming out towards us from the page and going away as well – and, of course, oscillating at all other angles as well. For a visual effect, take that wave and spin it, like an aircraft propeller, around the line of its movement (that is, around an axis going through the middle of the wave left to right on the page). This represents a real 3-D lateral wave, oscillating in every direction – unless it is held in a limited dimension by, say, a surface or line.

Now let’s look at our spinning sine-curve. You can notice two things: as you look left to right across the page, it has become a series of dark and light bands: dark where the slope from top to bottom is spinning, light were the peaks and troughs are spinning and there is much less ‘ink’. Also, you will observe that there is in the wave itself, no specific direction of oscillation, it is 3-D symmetrical.

This is a longitudinal wave, areas with more density alternating with areas with less density. Transverse waves in three dimensions are longitudinal waves. This is not just a visual effect but a reality: the wave is moving in one direction but the particles that make it up move as well in both other dimensions, 360 degrees. A lateral wave can only be achieved by removing some of the freedom of movement of these particles by, for example… putting the wave through a polariser.

While it is difficult to picture all this applying to a spherical wavefront, there are no actual challenges, other than the need for the polarisation to be communicated to the whole wavefront non-locally, an effect that has been specifically tested in the original entanglement experiments and found to happen

Now compare this with the general wave description of electromagnetic waves as alternating electrical and magnetic sine waves at right-angles to each other and the questions it begs:

1. What is varying in these two fields? That is, taking the peak of the electric field wave, what is there more of than when it is in the trough? Electrical potential?
2. Transverse waves vary in speed by wavelength and/or amplitude, so they are ruled out by the constant speed of F-waves.
3. Why do the waves go up and then down? With water waves they are pulled back to the middle by gravity, but here?
4. There appears to be two fields for the waves to move in at right angles. What are they and why are they at right angles? The analogy with the magnetic effect being at right angles to the direction of movement of electrons in a circuit exists but is totally different. There needs to be a reason why we are applying the same structure to an uncharged wave.
5. The wave is going in a specific direction. What chose this direction, how did it get its momentum and what got the opposite momentum to conserve the total?
6. The implication of this illustration is that polarisation would end up with a purely electric or a purely magnetic wave.
7. How is such a wave generated. The longitudinal wave with a spherical wavefront proposed by the heretics is naturally emitted by a ball-wave, such as an electron, shrugging off energy from its spherical surface.

The point of this is that, while you may have issues with taking on board the picture presented by the Heretics – and it normally takes about four readings for people to understand how longitudinal waves can be polarised, they are small indeed compared with the orthodox presentation.