The Second Heresy: The Field and the waves in it

In the first Heresy we saw that the Mitchelson-Morley, by showing that light in a vacuum always travels at the same speed, proved that it is a longitudinal wave, a type of wave that always travel at a speed dictated by the medium they are moving in.

Sound is a longitudinal wave and here we are suggesting that electromagnetic waves like light are longitudinal waves too.

We need to put to bed another false lead. Light waves are often illustrated as transverse waves, like water waves, see example below, or as two transverse waves at right-angles to each other, one electrical, one magnetic. There are two problems with this: the speed of transverse waves varies according to their amplitude – big ones go faster and they are not possible in a 3-D environment without there being an existing 2-D surface, like water, or (pseudo) 1-D line, such as a rope, to constrain the wave to fewer than three dimensions.

To illustrate why, consider a classic transverse wave, like the sine wave below:

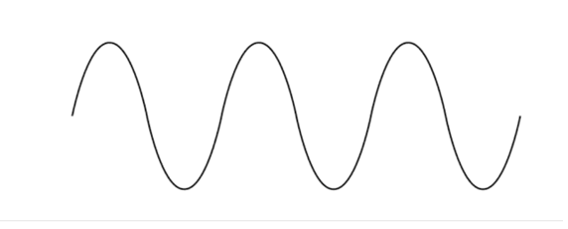
In a 3-D environment, this can be considered as a thin vertical slice from a wave that is actually coming out towards us from the page and going away as well – and, of course, at all other angles as well. For a visual effect, take that wave and spin it, like an aircraft propeller, around the line of its movement (that is, around an axis going through the middle of the wave left to right on the page). This represents a real 3-D transverse wave, unless it is held to a limited dimension by, say, a surface or line.

Now let’s look at our spinning transverse wave. You can notice two things: as you look left to right across the page, it has become a series of dark and light bands: dark where the slope from top to bottom is spinning, light were the peaks and troughs are spinning as there is much less ‘ink’ in these areas. There is no specific direction of wave oscillation, up/down or side-to-side, it is 3-D symmetrical. Nor do the particles that make up the wave, air molecules in the case of sound, move preferentially in any specific direction other than in the direction of the wave’s travel.

This is a longitudinal wave. Transverse waves travelling in all three dimensions are longitudinal waves.

From now on we will now rename ‘light and other electromagnetic waves’ and refer to them as ‘fundamental waves’ or ‘F-waves’. The ‘electromagnetic’ part of the previous name is both cumbersome to say and presumes something about how the waves work that we will come to question. F-waves cover every wavelength from long radio waves to fantastically short cosmic rays, but they are all of the same basic type. The shorter the wavelength, the more the energy a wave has.

We will call the medium through which fundamental waves travel the ‘Field’, capital F, for the fundamental field of the vacuum. Finally, we will call the speed that F-waves travel in a vacuum the ‘speed of the Field’ – a better term than the ‘speed of light’, as light goes different speeds in different mediums[1]. The speed F-waves travel is set by the Field at 0.3 metres per nanosecond or 3×10⁹ms^-1 in the vacuum.

We know only three things about the Field:

1. Parts of the Field can have values higher or lower than the average value of the field. This is the minimal requirement for waves. Fundamental waves are formed by alternating areas of lower and higher Field values (shortened to lFv and hFv) moving through the field at the speed of the Field. We do not know what these values are or what they mean, only that they can vary and are opposed to each other around an average value. This is analogous to air pressure and sound: sound waves are formed by waves of lower and higher than average air pressure.

It is almost certain that the Field is granular, that it comes in separate defined tiny ‘units’. If it were not, we get troubled by infinities, infinitely small things and, while infinities have mathematical uses, they cannot physically exist. The Heretics find it most useful to think of a ‘unit’ of the Field as occupying a very similar role to a molecule in air but without any mass. This ties in with the Planck constant, the measure of the minimal size, the original ‘quantum’ relating to one single unit of the Field. We will refer to these as ‘Field units’

2. The Field values of units are affected by the values of their neighbouring units. Where two neighbouring Field units have different values, the ‘No Special Place rule’ tends to equalise their values. This means that Field values tend to converge on the average. But, like all waves, higher or lower Field values that start off moving towards average Field values will overshoot that average, much as a pendulum is attracted down from the highest point of its swing towards the bottom of its swing overshoots, going up the other side again and again. This pattern of alternating high and low values moves through the field as the Fundamental wave (F-wave). It does so as an expanding sphere, the wavefront, away from its point of origin but, like sound, reflects off surfaces. There is no friction in the field, so a wavefront goes on expanding forever if nothing disrupts it[2]. The time taken for one Field unit to affect its neighbour is what determines the speed of the Field – 0.3m per nanosecond in a vacuum, slower where there is matter and the denser the matter, the slower the speed[3].
3. The field is not still but is like a choppy sea, with patches of higher and lower values. There is no reason for it to be smooth or flat and it has many waves passing through it. We can detect these as the ‘vacuum fluctuations’. We will call these ever-changing areas of higher and lower values ‘bubblets’ because they are like bubbles in a moving foam. Like bubbles in a foam, they probably form roughly spherical but actually polyhedral shapes, changing constantly. There are also little vortices in the field called ‘neutrinos’, rather like ‘dust devils’ or the small whirlpools you sometimes see in streams. Later, we will see how bubblets of differing values, forced into patterns, become the electrical and magnetic charges. In Feynman diagrams, bubblets are called ‘virtual photons’, popping into and out of existence.

An F-wave is a succession of areas of low and high Field values moving through space at the speed of the field. These changes move outwards from the origin of the F-wave (often an electron), forming a spherical wavefront expanding at the speed of the Field outwards. Because the wavefront is spherical, the overall momentum of the wave is zero, the total momentum of its expansion cancelled out by opposite points on the sphere moving outwards in the opposite direction. When the wavefront hits things that prevent it passing, it reflects off them and deforms from its original spherical shape, just as a sound wavefront does. If the object is small enough, the wave will pass it by, slowed down slightly. This is what causes refraction. If the wave hits an object it harmonises with, such as an electron in an atom (electrons’ wavelengths in atoms vary, see the Third Heresy), it transfers its kinetic energy to that object, much as a sound wave transfers its energy to your eardrum. This transfer of energy does not transfer momentum because the energy goes to makes the electron’s ball-wave (see Heresy 3) get larger all round. This means that ordinary light is simply absorbed by the electrons in atoms and, generally, emitted out again. When the F-wave harmonises with an electron, all the energy of the wave transfers at one point, however large the wavefront has become.

The energy of all types of waves, water waves, sound waves or F-waves has no specific location – it exists as the difference between the ‘peak’ and the ‘trough’, between the pulses of hFv and lFv in longitudinal F-waves. The energy has no specific location but is in the whole of the wavelength, just as much with water or sound waves as F-waves. When an F-wave hits several electrons that it can harmonise with – electrons are much smaller than light waves – all its energy will go to only one of the electrons  but which electron will get the energy seems impossible to determine: the energy lies within a wavelength but where in that length the transfer takes place seems random. This fact accounts for much of the complication of QM calculations and the old idea that, to do this, the wave must transform into a ‘particle’. While the point on the wavelength at which any type of wave transfers energy is unpredictable – although many transfers add up to a predictable pattern. This is one way the ‘Heisenberg Uncertainty Principle’ is expressed and is emphasised by the next aspect of fundamental wave behaviour.

In one crucial respect F-wave behaviour does not resemble sound wave behaviour. As a sound-wave’s spherical wavefront propagates outwards, it becomes quieter, it’s amplitude decreases, because, as its wavefront gets larger, its energy must move an ever-increasing number of air molecules. This does not happen with F-waves, which are the smallest thing of their type and cannot break into bits. Their wavelength and amplitude stays the same as the wavefront gets larger although they can still only be absorbed at one point. This picture was thought impossible until the proof of entanglement around 2015 and is still quite new. The wavefront of light from a distant star may be thousands of light-years in diameter but will still be absorbed by one atom in your eye – which is why you can see the star.

Another key difference between soundwaves and F-waves is that all sound waves can vary in ‘volume’, amplitude, but it seems that only the longer F-waves – radio waves for example, vary significantly in volume. While this maybe in part because it is very difficult to measure the amplitude of small f-waves like light, their variation cannot be great, or it would have noticeable effects. It seems that all but the longest F-waves – microwaves and radio waves – are so compressed that they look like a bar-code anyway, with very sharp changes from low to high Field values and vice versa, so amplitude cannot be significantly increased[4]. As a result, variations in the energy of waves come almost entirely in the form of variations in wavelength: longer wavelength = less energy, shorter wavelength = more energy. (This is true of sound waves as well, but the energy variation of amplitude is generally larger than the energy variation of pitch in sound.)

The fact that F-waves behave like waves but are absorbed at one point for a long time encouraged a rather zany picture of light as a wave that transformed into a ‘particle’ of zero size the exact instant it was absorbed by an electron, or, rather, that the many probable locations of the virtual particle collapsed into an actual location. The concealed assumption behind this was that ‘probability collapse’ of a wave could move faster than light speed.

However, we can demonstrate with a simple, homely experiment a wave spreading across a large area, then vanishing into the choppy background after absorption at a single point. This also demonstrates probabilities collapsing non-locally, so fits the type of mathematical model used for F-wave calculations.

Start with a small domestic tropical fish tank and carefully make sure it is horizontal before you fill it to the brim with water. Then use a pipette to release one drop of water about 5 cm above the centre of the tank (we used one with a squeezy bulb from the top of a bottle of ear-drop medicine). You will see ripples (waves) spreading out from the point where the drop lands. Then, if you have got it just right, you will see one drip of water spill over the side. (This is much easier to set up than you might think. The biggest problem is to spot the drip, but you can put coloured paper around the side to act as a ‘drip detector’.[5]). A wide, circular wave has collapsed at a random point and the possibility of another drop emerging anywhere in the tank has vanished in that instant. Presumably, this would be true however large the tank involved, although stopping random factors interfering would become increasingly difficult. You could, if you wanted, describe what happens here using the math developed by Heisenberg, with the ripple generated by the original drop presented as a ‘wave of drip probability’. Or, coming more up to date, you can describe the ripples as Feynman does, as a pattern of virtual drips that take all paths between the point of origin and the point the actual drip appears. The wave model of fish tank and its transformation from wave to drip has the same result in the ‘sum-over-paths’ Quantum Electrodynamics Feynman developed, as well as in Heisenberg’s probability waves.

‘Non-local’ means that two or more linked things happen at the same moment, regardless of how far apart they are. It was regarded as impossible because it was believed impossible for any connection to work faster than the speed of the Field (a.k.a. ‘the speed of light)’. But it has now been demonstrated and, since about 2015, the experimental results have been so convincing that all but the crustiest physicists now accept non-local connections, using the term ‘entanglement’ for the demonstration of the phenomenon[6]. It is also probably fair to say that, now that we no longer regard the ‘speed of light’ as a mystic number but simply the speed of the vacuum Field, the shock of instant reaction at a distance becomes less dramatic. No longer is ‘Spacetime’ an ‘Absolute’, it is just the speed that waves in the Field move at.

As we touched in earlier, the previous models of F-waves also required faster-than-light processes, but this was concealed by referring to the instant absorption of F-waves as the ‘collapse of the wave equation’. This is a mathematical process that, like all mathematical processes, takes no time, so instant transformation was achieved without saying so.

Just as an F-wave must harmonise with a particle (such as an atom or electron) to be absorbed by it, so F-waves can only be emitted by particles at their harmonic wavelengths. This need to harmonise, both when emitting and absorbing fundamental waves, means that waves are only emitted and absorbed at specific wavelengths, just as a musical instrument only emits sound waves at specific wavelengths[7]. This accounts for the ‘quantised’ nature of emission that Plank used to calculate and resolve the problem of ‘black body’ emission in 1900 and the quantised transfer of momentum Einstein used to resolve the ‘photoelectric effect’ in 1905.

It seems that the picture of fundamental waves as longitudinal waves in the Field, as well as explaining the Michelson-Morley result, also works with all the existing math of quantum mechanics. It is just a simpler way to think about the things the equations are talking about. Picturing F-waves this way makes the finding of the two-slit experiment entirely expected. If you split a wave through two slits and allow the two resulting curved wavefronts to interact, they interfere. Hitting a detecting wall, they show a pattern of alternating density areas. This is what we observe with waves, with sound waves and water-waves treated the same way. But you consider light to be particles, they should go through the slits like bullets, forming a cluster, densest at the centre. Observing the interference pattern that results from the two-slit experiment conflicts with the particle model.

Lots of other observations are simple in the world where ‘electromagnetic waves’ are simply longitudinal waves in the Field. If you look at a typical microwave oven, you will see a glass panel in the door that enables you to see what is inside the oven. But you will also see that the window is covered with little round dots. These are metallic and microwaves bounce off metal, like the metal of the oven interior. However, microwaves, like light waves, go through glass without trouble, so why do the microwaves not come out though the glass door as the light does? The answer is that the metal dots on the microwave door are placed so that the distance between them is (a lot) shorter than the length of the microwaves used, which normally have a wavelength of around 7 centimetres (light, with a wavelength of around one billionth of a metre, has no problem going between the metallic dots.) As the whole of the microwave cannot get through between the dots, none of the microwave and none of its energy gets through.

To those of us familiar with the larger world, water and sound waves, the question immediately arises, ‘Why doesn’t a bit of the wave get through the gap between the metallic dots? They are around 1cm apart and the wavelength is around 7cm, so there should be wriggle-room?’ Alternatively, ‘How can the wave ‘know’ that it is not going to get through, when the first less-then-one-seventh has already ‘started to escape’. There is an ‘all-or-nothing’ quality about light and other fundamental waves that comes from their nature as a pattern: once the pattern is broken there is nothing, not a part pattern. A few people standing up in a stadium is not a ‘Mexican Wave’.

Another example of ‘quantum mysteries’ that vanish: if you blow gently down a ‘penny whistle’ or across the top of an open bottle, you will get a lowish harmonic note. Gradually increase the pressure of the blow and the volume of the low note will rise until, suddenly, the note will jump up an octave. This is because at a certain point, the extra energy of the harder blow cannot be absorbed by the wavelength of the low note but needs a shorter wavelength that can hold more energy. The next wavelength that fits in the whistle or bottle is one half the length of the low note we started with. This we hear as an octave higher. But it jumps from the first wavelength to one half the size without going through the intermediate notes, as their pattern cannot exist. In the context of fundamental waves, this is often called ‘A Quantum Leap’, but it is no different to the leap made by the penny whistle, and every musical instrument.

All this lengthy discussion is to explain how it can be that there is either a harmonic, the waves fit together in a matching pattern, or there is nothing. Either a whole wave gets through the window of the microwave of none of it does. Where there is a harmonic, action may be achieved on a larger scale – the transfer of kinetic energy, for example – where there is not a harmonic, nothing happens on a larger scale. This also applies when a wave is absorbed – once the kinetic energy is transferred from the wave to the object it has harmonised with, the wave ceases to be and whatever movement remains is just part of the background turbulence of the field.

With sound waves, this is what your eardrum harmonises with and absorbs some of the kinetic energy of a sound-wave.  But here the example of sound can be misleading for F-waves. The big, human sized, world is full of soft things that can absorb a huge variety of different wavelengths. In the fundamental world, objects can only absorb the very limited range of wavelengths they harmonise or resonate with (in this context they mean the same thing). For an electron in an atom to absorb the energy of a light-wave, it must harmonise with it, it must have a very specific wavelength that is related to the length of the light-wave[8]. Normally such an electron will have quite a number of different light wavelengths it can resonate with but they will all be specific and, if the light-wave has a different wavelength to any of them, it will not be affected by the electron (except to be slowed down a bit).

Unless they harmonise, waves quite happily pass through each other. You can see this on the surface of choppy water, as the wake of a boat passes through the small waves. Sometimes they hit a flat, vertical surface, like a concrete harbour wall and reflect and you can see them passing back through the wake waves behind them. When you listen to a band or orchestra, the sound waves made by the different instruments arrive at your ear independently through the same space, as you can tell by distinguishing individual instruments and singers from the whole sound.

Returning to the other F-wave interactions, we have discussed the simple way F-waves bounce off things and their absorption when they harmonise with an electron in an atom. At higher energies, an energetic F-wave can transfer momentum. It hits and resonates with an electron and kicks it out of an atom in the ‘photelectric effect’ or, at higher energies still, it can transfer a large part of its momentum to the whole atom, giving it a kick-start, in what is known as the ‘Compton Effect’. You can see a similar effect of energy transfer with powerful water-waves. These do not reflect off a vertical wall or rockface, as weaker waves do, but hit them with almost explosive energy, throwing spray high into the air.

In both these cases, not all the energy is necessarily transferred, the F-wave in the Compton effect going on after kicking the atom but with a much longer, less energetic wavelength. In the case of electron/positron pair formation, any excess energy goes into accelerating the two particles.

In the photo-electric and Compton effect, the F-wave must conserve momentum, so either the wavefront needs to hit two electrons on opposite points of the wavefront or the original object that emitted the wave must recoil to match the momentum gained by the electron. Both seem possible, and both need to be ‘non-local’ effects.

Finally, at very high energies, above 1.022MeV, F-waves turn into a paired electron and positron, about which we will have much more to say later. For the moment it is worth noting, however, that this process only happens if there is a nucleus nearby to ‘recoil’ and absorb the momentum of the wavefront. This is the most tangible example of the non-local transfer of momentum that we need to make the Compton and photoelectric interactions work.

These then are the different interactions an F-wave can have – reflection, slowing when passing through and between particles, harmonisation/absorption, transfer of momentum to electron or atom – and ‘pair formation’.

Waves are emergent phenomena; they only exist as patterns of smaller things. If you look at the individual bits that make up waves, the gas molecules in sound waves or Field units in F-waves, whether they are in a wave or not does not change them. Sound does not happen at the level of individual air molecules; it exists as patterns of large numbers of molecules. Waves are only seen when a group – often a very large group – of the individual bits are considered – the same applies to ‘entropy’, equilibrium and other emergent patterns and groups or patterns that can vanish or change without regard to distance or time, even patterns as simple as the drips from a fish tank.

A good example is a ‘Mexican wave’, a wave of people standing up in a football stadium that moves around the stadium at a definite speed. However, several individuals standing up at once is not ‘part of a Mexican wave’ it has nothing wavelike about it, it is just part of the background turbulence. This character of waves perhaps makes the ephemerality of F-waves more comprehensible.

Another way to think of this is that a whole pattern can change to a different pattern with just a very limited change in the bits that make it up. Here is an example:

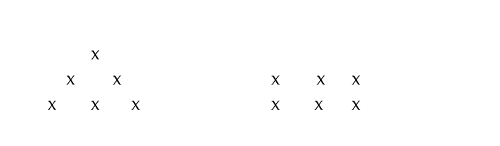
The change of pattern from a triangle to a rectangle is caused by small, unchanged, elements moving a small distance. A similar, small degree of change to a wave, especially if it transfers energy elsewhere, can have just as large an overall effect on the complete emergent phenomenon, changing the wave into simply another bit of choppiness in the Field. This means that F-waves are an all-or-nothing phenomenon in much of their behaviour, not just in absorption. You can’t have part of a wave, such a ’part-of-a-wave’ is just part of the background choppiness, a bubblet of divergent Field values, like all the other bubblets.

So that is the heresy: light is not a mystic probability wave that turns into a particle for zero time at the point it is absorbed by an electron – which is as close to a description of the orthodox view as we can get. It is simply a longitudinal wave with a spheroidal wavefront, much like sound, mostly initiated by a vibrating ball-wave (as we shall see), its speed fixed by the medium it travels in. The vacuum of space is filled with the Field and that determines the speed of wave travel through it. F-waves travel more slowly through thicker media such as water or glass.

Before leaving F-waves, we do need to note an unanswered question. Our waves have a feature, known as ‘spin’ that we have ignored entirely. This is quite like spin as we know it in some ways and in some ways not. It is covered, at least in part, at the end of the third heresy on the ‘Waves that make Matter’.

Anyway time to move to the third heresy: how matter is made.

[1] The English plural of ‘medium’, mediums, is less confusing than the Latin plural ‘media’, which often refers only to edited communications.

[2] The wavefront is ‘entangled’, such that if a bit of it is absorbed, the whole wavefront effectively vanishes. So, unlike a sound wave, it does not get ‘quieter’ as it expands. We will give detail on this later.

[3] Matter acts like a series of small blockages to F-waves, so slow their speed. The denser the matter to sound waves, the close the molecules are to each other, so the faster sound travels.

[4] FM radio waves are around 2-3 metres long, light waves are around 500 nanometres long, around ten million times shorter.

[5] Ignore any times that you get two drips or no drips. This has been called cheating by some, but it simply ignores those experimental runs where you have not got the conditions exactly right. If you knocked the whole apparatus over, you’d ignore that result!

[6] Not all physicists had thought it impossible. One of the great founders of Quantum theory, Louis de Broglie (pronounced ‘de brolee’) put forward a non-local theory in 1927 (pictured as a ‘pilot wave’). This was revived by David Bohm in 1952. It was fascination with this idea that prompted John Stewart Bell to propose ‘Bell’s Theorem’ which gave the theoretical impulse to the development of the experiments that proved non-locality. Heresies often have deep roots.

[7] A horn or penny whistle that goes from one note, say middle C, to a note an octave higher, upper C when it is blown harder, has done a ‘quantum jump’. It has moved from one wavelength to another, half the length, without going through the intermediate lengths.

[8] We shall see later that electrons are a kind of wave themselves, albeit one that goes in-and-out rather than along, so they have a basic amount of energy that a light wave can add to if it harmonises. Their wavelength when they are in an atom varies according to the size of the atom, so they absorb different wavelengths of light.